First week through Guided Practice and Peer Instruction

I have completed the first week of classes. I also took a good 36 hours to sleep and play with my children, so I am feeling up to getting back to work. The retooling of my liberal arts mathematics course to handle 70 students involved a lot of work. My usual work pattern involves long stretches of thinking and indecision, followed by a short, intense burst of actual production. I had to repeat this for every class meeting this week, so I was very tired on Friday. Labor Day weekend is well-placed for me this term.

So, how did the big experiment with Guided Practice and Peer Instruction start? More after the jump.

Recruiting Workshop: Picture Hanging Puzzles

Today was Math Day at UNI. This is a big event where the department invites lots of prospective students with strong records and declared interest in some flavor of mathematics major to come visit and be amazed by how awesome we are. The day includes a fancy lunch, and (for the students) a little test used as part of scholarship screening, some activities with faculty members, (and for the parents) discussion of financial aid, presentations on possible career choices, and a campus tour.

I ran a short workshop (activity?) for prospective students. I have done this for five years running, now, and I am starting to build up a repertoire of fun demonstrations and investigations for dealing with a students with a high school background. I like to use topology topics because there are lots of mind-bending things one can do with no background: ideas that are interesting, immediately understandable, and hands-on.

Mathy Activities

Originally Posted 02-01-2012

Tomorrow involves several non-standard bits of work for me. UNI is hosting 31 prospective undergraduate students and their parents for the day at an event we call MathDay. Also, it is time for another math club meeting.

Math Day Recruiting Activity

A big part of math day is the salesmanship of some little activity workshops we run for the students. Last year’s was particularly successful so I am going to use it again. Now, the important thing is the performance, and last year, man, I was on: wit, charm, energy, humor. I hope it goes as well this year. the activity is fun enough on its own to survive no matter what, but it is simple enough that I can give it to you in two sentences.

First bisect a Moebius band to get a longer Moebius band (still one piece!). Now explore generalizations with different numbers of half twists or different types of cuts.

This is stolen adapted from an old Martin Gardner Scientific American column called Mathematical Games. It is fun, just weird enough that you have to try it yourself to see how it works, and straightforward enough that you can make a clear conjecture inside of forty-five minutes.

Math Club

I recently learned a neat theorem by John H Conway and Cameron Gordon (I think I am remembering that correctly) that says any embedding of the complete graph on six vertices into three dimensional space must contain a pair of linked triangles.

This is just plain awesome. I am still working on a plan, but it might involve some play-doh and shoestrings. Or maybe it should be pipe cleaners.

Anyway, both are good topics for engaging students. Use as enrichment or as a hook.

Outreach?

Another odd thing is that a local high school teacher had a student give a proof that 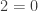using complex numbers. He wrote the department, and somehow I got picked as the person to answer his plea for help.

It is a fun one, so I’ll just leave the argument here and let you puzzle it out.

Anthony’s Paradox