The Big Unteaching Experiment: Rebooting the Machine

OK. Sorry for the confusion earlier today folks. I accidentally posted things meant for my classroom blog to this one. And they got automatically tweeted out. Awesome. So, now you know that I keep a simple blog for my students each semester. That way we all have a running account of what happens each day. I find it especially useful for my Moore Method geometry course, but it serves well if a student might happen to miss a meeting.

We are now past the half-way point in the semester. In fact, spring break starts right about…now. I have been worried for some time about the state of my experimental differential geometry course, and today I discussed with my students how we will go forward in a manner different from the first half of the term.

Things I Need to Run Differential Geometry

Time to get down to brass tacks. What things do I want to have in hand at the first meeting of my differential geometry course this semester? What things must I create before I meet the students so that everything can run in an orderly fashion? (Given the course structure, I am using the word “orderly” in a rather loose sense, here.)

• An Official Syllabus: this is the document required by state law. It has to have certain things on it.

• An IT structure for dealing with recording student achievement and demonstrations of competence. (Somewhere between “scattered pieces of paper” and “My own web-app grade book database with customized reporting options.”)

• The first assignment: this is the one that gets students rolling towards making an overview and choosing their learning goals.

• My own outline of how to handle phase one of the course: the theory of curves in the plane and in space.

• A set of ideas for projects (Josh Bowman helps me here)

• A list of examples to fill out my “example a day” plan.

• A tightly controlled structure for a warm-up project to help students get over the disorienting freedom I will give them. (With great freedom comes great responsibility, or something like that.) (Patrick Honner helps me here.)

• An annotated bibliography to share as a guide to the available literature students might use to get started. This will lean on my book review project, which is languishing right now. I will do a few more in the next week.

• Something to guide my students through the “advanced calculus gap.” I don’t need real analysis, I don’t need full-blown differential topology, but I do need more than the standard multivariable calculus and linear algebra courses require. Spivak’s Calculus on Manifolds is probably aiming too high. I have a copy of Shifrin’s Multivariable Mathematics, so I will look through that. I might have to make my own thing here. I hope not.

• Speaking of Shifrin, I need to arrange the latest of edition of his undergraduate diff geom book as a course pack for the students.

• Some way of carting my stack of books to class each day. Seriously. I need to figure out a mechanism for getting my undergraduate level differential geometry library from my office down to the classroom. I need a cart, or a bunch of sturdy square bags or boxes with handles.

• A killer opening. I want to grab attention with the first twenty minutes. This stuff is seriously cool, and I want to build a little excitement for the material.

• Some serious spine-stiffening. I have to present this craziness, and I have to do it in a self-assured and encouraging manner.

Have I missed anything? I think I can have half of these squared away by the end of the day on Friday, with good progress on the others.

Objectives for Differential Geometry

Regular readers (all three of you) are aware that

1. I am scheduled to teach differential geometry this coming term.
2. I am very excited about this.

a minimal surface

Less well known is that I am also terrified of this experience. I taught the course in the Spring of 2010 and the experience was not all warm and fuzzy. The biggest problem was the disconnect between what my students knew coming in, and what I thought they would know. Suffice it to say that I have a much better understanding of what it means to have a student who passed linear algebra and multivariable calculus at UNI.

Let’s take it as given that this iteration of the course will also contain surprises, but I hope they will be much smaller ones. And I am at a place now as an instructor where I am much more alert for this kind of trouble, so that can only help. (Oh, please, please let that be a true statement.)

So, now I have spent a fair amount of time in the last two weeks worrying about how this course will all work out when I should have been properly enjoying time with my family. I started by trying to write a set of learning goals for the students.

An Outline for Undergraduate Linear Algebra

Over on the Google+, Dan Drake inverted my challenge to mathematics education faculty. He asks, how can mathematicians share what we have learned?

This is an excellent question, which is pretty hard to answer. Since this is my blog, I’ll follow Pólya’s advice, and attack a simpler problem that I still can’t solve. What is the point of each course in the undergraduate mathematics curriculum?

Linear Algebra

A few weeks ago, I wrote about the real point of linear algebra. As usual, that flash of insight was half-baked. I still stand by it, but I’ve been thinking about the course more as it goes on. Here is a fuller description of what I hope to accomplish in a one-semester linear algebra course at the University of Northern Iowa.

Meta-mathematical goals

Every mathematics course should work on core fundamental skills of mathematical process. In linear algebra, I think the two foremost issues are:

• making examples for yourself to gain understanding, and
• gaining comfort with increased levels of abstraction.

Let’s add another item to this list that I think is important:

• learn the use of modern computational tools to do intensive computations and produce visualizations. (Of course, I am using Sage.)

Content Goals

I would like for students to understand the following.

• solving systems of equations
• vector algebra
• algebra of matrices
• matrices as transformations
• the geometry of euclidean space as encapsulated by the dot product
• determinants
• Gram-Schmidt & orthonormal bases
• eigenvectors and eigenvalues
• “some associated geometry”

I’m not sure anyone would argue with these. Of course, this list leaves a lot out. And I hid a lot inside “some associated geometry.” For starters, the ideas behind a set of vectors being a basis or not are really geometry.

A Skeleton Plan: A Course in Three Acts

Here is how I now view the structure of the course. I am just now finishing up Act Two, so the last bits are just a plan.

Act One: Ways To See A System of Equations

The first part of the course focuses on understanding the various ways to interpret a system of $m$ linear equations in $n$ unknowns.

1. The ‘row picture’: view the system as defining hyperplanes in
2. The ‘column picture’: view the system as defining an equation expressing some vector as a linear combination of 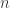vectors in .
3. The ‘transformational picture’: The system defines a “matrix-vector equation” .

As part of this, we study the geometry involved, make lots of pictures and try to get a sense of how these things hang together. We will introduce the idea of vector and matrix algebra, including the difficulties of matrix algebra, the dot product, and the cross product in . There are basic properties to investigate, and some problems to formulate, including the basic problem of invertibility for square matrices.

Act Two: Gaussian Elimination and its Uses

This part of the course is all about how Gaussian Elimination works, and the myriad ways we can leverage it to learn about all of the problems we’ve set ourselves. I think you can hit things like this:

1. Solving systems of equations
2. linear dependence and independence, the idea of a basis
3. the column space, kernel, row space and left kernel appear
4. the LU decomposition of a matrix
5. matrices as products of elementary matrices
6. the rank-nullity theorem
7. the determinant (I use a geometric definition)
8. the invertible matrix theorem
9. the general idea of a vector space and of subspaces
10. the nature of a matrix as a function

Act Three: Inner Product spaces

This final part of the course is devoted to extra structure we can glean using the tools we have built so far. The major ideas I think one should hit are these:

1. Gram-Schmidt and orthonormal bases
2. orthogonal matrices
3. the QR decomposition? (maybe not, but it is right there)
4. eigenvectors and eigenvalues
5. the finite dimensional spectral theorem

The Appendix: Cool Stuff

If there happens to be time…

1. The PageRank algorithm
2. Curve fitting
3. Image Compression

Comments?

At this point, I think I have a decent set of materials for Act One, a realized plan of attack for Act Two (with materials that need some work), vague plans for Act Three, and some stuff for the appendix already built.

I believe that I will take some versions of my materials and turn them into Sage-enhanced monographs. This will take a significant amount of work, but I can reuse that stuff to support future instances of the course. I hope those future instances will be more inquiry-based.